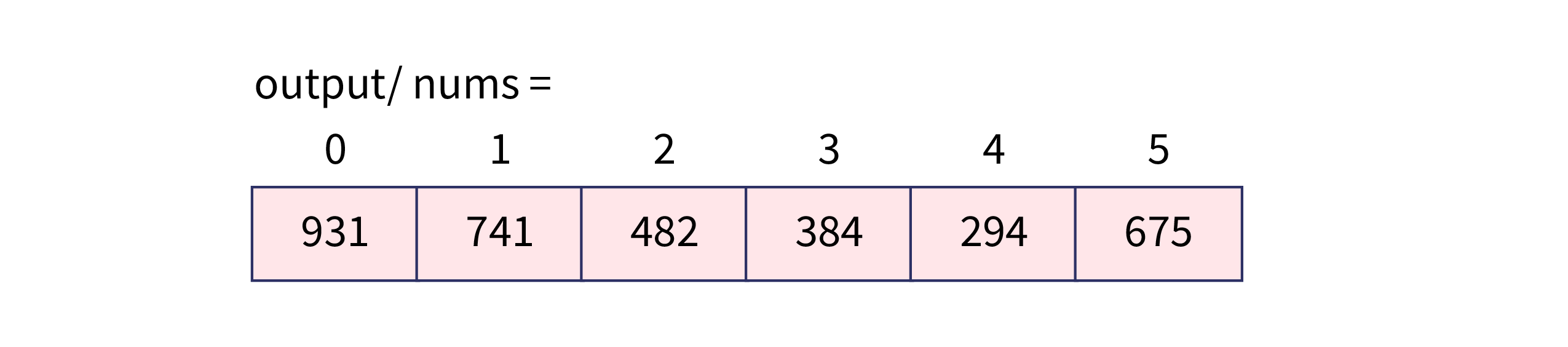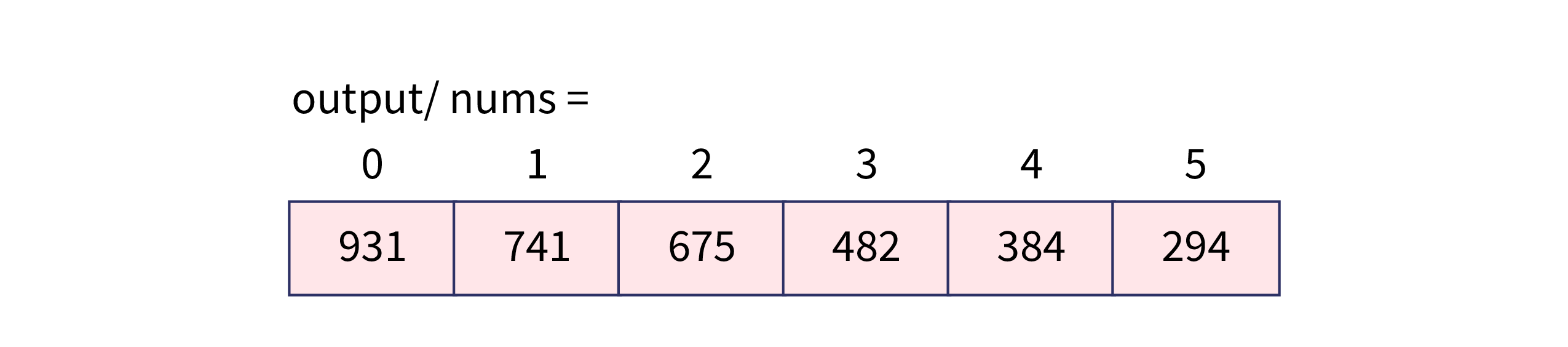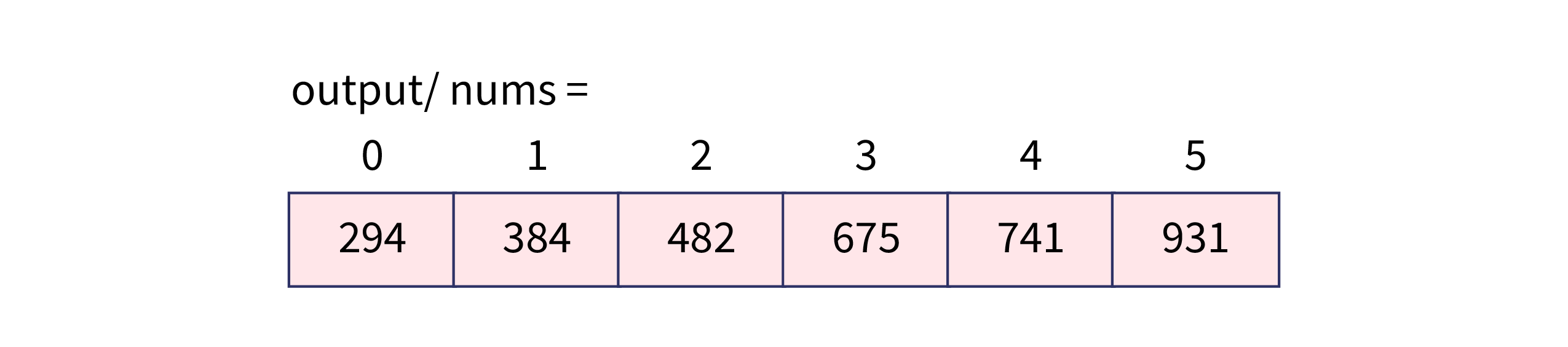
public class RadixSort {
public static void radixSort(int[] arr) {
int max = Arrays.stream(arr).max().getAsInt();
for (int exp = 1; max / exp > 0; exp *= 10) {
countingSort(arr, exp);
}
}
private static void countingSort(int[] arr, int exp) {
int n = arr.length;
int[] output = new int[n];
int[] count = new int[10];
for (int i = 0; i < n; i++) {
count[(arr[i] / exp) % 10]++;
}
for (int i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
for (int i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
System.arraycopy(output, 0, arr, 0, n);
}
int getMax(int arr[], int n) {
int max = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] > max)
max = arr[i];
}
return max;
}
void countSort(int arr[], int n, int exp) {
int output[n];
int count[10] = {0};
for (int i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;
for (int i = 1; i < 10; i++)
count[i] += count[i - 1];
for (int i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
for (int i = 0; i < n; i++)
arr[i] = output[i];
}
void radixSort(int arr[], int n) {
int m = getMax(arr, n);
for (int exp = 1; m / exp > 0; exp *= 10)
countSort(arr, n, exp);
}
int getMax(int arr[], int n) {
return *max_element(arr, arr + n);
}
void countSort(int arr[], int n, int exp) {
int output[n];
int count[10] = {0};
for (int i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;
for (int i = 1; i < 10; i++)
count[i] += count[i - 1];
for (int i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
for (int i = 0; i < n; i++)
arr[i] = output[i];
}
void radixSort(int arr[], int n) {
int m = getMax(arr, n);
for (int exp = 1; m / exp > 0; exp *= 10)
countSort(arr, n, exp);
}
def getMax(arr):
return max(arr)
def countingSort(arr, exp):
n = len(arr)
output = [0] * n
count = [0] * 10
for i in range(n):
index = (arr[i] // exp) % 10
count[index] += 1
for i in range(1, 10):
count[i] += count[i - 1]
for i in range(n - 1, -1, -1):
index = (arr[i] // exp) % 10
output[count[index] - 1] = arr[i]
count[index] -= 1
for i in range(n):
arr[i] = output[i]
def radixSort(arr):
max1 = getMax(arr)
exp = 1
while max1 // exp > 0:
countingSort(arr, exp)
exp *= 10